こんにちは!塾長の坂根です。
今日は、以外と大事な『切片』について解説します。
『切片』というと、中学数学ででる一次関数の『傾き』とセットで覚えたものですね。
しかし、この切片が一次関数しかないと思っている人がけっこう多いです。私の塾の教室に来ている高校生の生徒さんの半分ぐらいが勘違いしています。
まず、『切片』とは「y軸でグラフが交わる場所(座標)」のことを指します。(指数関数や三角関数のグラフは除きます)
実際のグラフで見てみると、
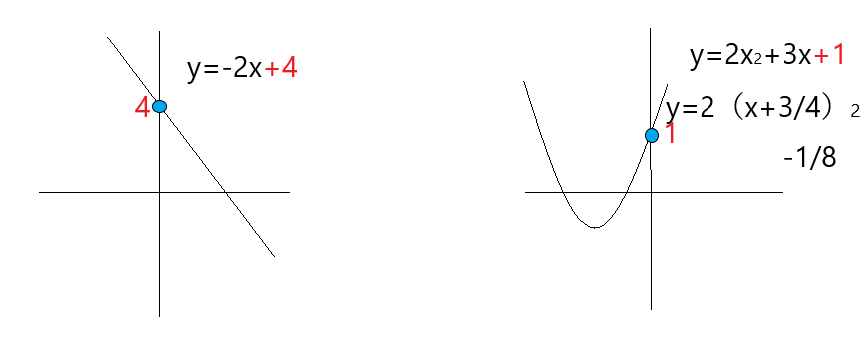
左側の一次関数のグラフは皆さんが一番よく知っているものですね。そして、右側の2次関数のグラフにも切片があるのがわかりますか?
さらに、3次関数にも切片があります。下のグラフを見てください。
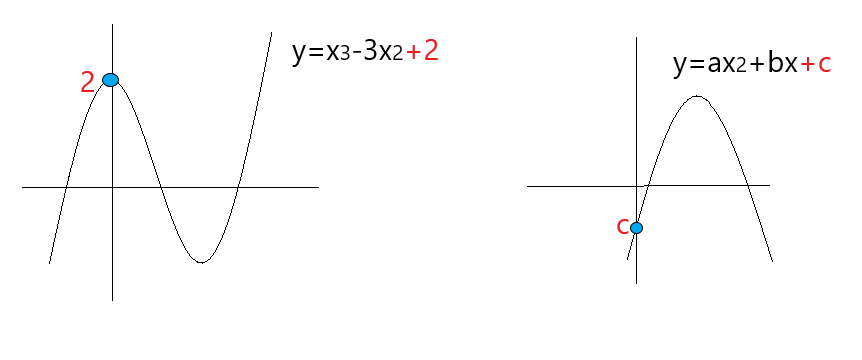
もうお気付きだと思いますが、切片とは次数(xのような文字)がない数字のことを指します。
切片はy軸で交わる=xが0のときのy座標のことです。なので、何次関数であろうと、グラフはy軸上で次数がない数字を通ることになります。
このことを知っていると、色々な問題に応用できます。例えば、
「関数 y=2×2(2xの2乗)+ax+a+1のグラフは点(0,4)を通る」
と問題に書いてあるとすると、「点(0,4)を通る=切片が4」だとわかるので、
「a+1=4 つまり a=3」
ということになります。
また、2番目の右側のグラフのようにすべてが文字になっていたとしても、切片がy軸のマイナスゾーンにあるので、「切片=c<0」ということもわかります。
数字のグラフ関連の問題では、切片や傾き(変化の割合)を正確に書かないとわからない問題もたくさんあります。なので、この記事だけでかなり正確なグラフが書けると思います。
以前書いた『傾き』の記事も合わせて読んでいただいて、数字の基礎を押さえておくと解ける応用問題もたくさんあるので、いま一度基本に立ち返ってみましょう!



