こんにちは!塾長の坂根です。
数学に何度も出てくる『絶対値』。
今日は、わかっているようでよくわからない『絶対値』について理解していきましょう。
絶対値の攻略は、まず絶対値が本来どういう意味を表しているのか知ることからスタートします。
絶対値の基本的な考え方は下の図の通りです。
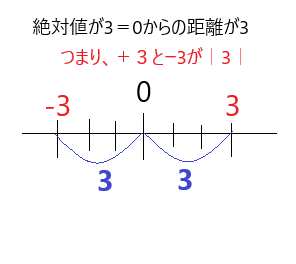
『絶対値』とはべつの言葉に言い換えると『距離』を表しています。
上の図のように、0からの距離が3の地点(座標)はどこかと言われたら、「±3」の地点になりますね。
ここでポイントなのは、『距離』という概念に「マイナス(負)」は入っていないことです。
高校1年の最初らへんの数学で、|3|も|-3|も答えは「3」になると教わりませんでしたか?
なぜ|-3|も「3」になるのか、それは絶対値は『距離』を表しているからなのです。
次に、|-3|の答えが「3」になるまでの過程を式にするとこうなります。
『|-3|=-(-3)=3』
(-3)を+3で答えとして出すには、『-を(-3)にかける(つける)』必要があります。
つまり、絶対値の中(|x|のx)がマイナス(負)のときは必ず『-をつけて絶対値を外す』というこです。
この理屈がわかると、次の問題の解き方がわかります。
『|√2-2|=-(√2-2)=-√2+2』
√2は約1.4で、「1.4-2=-0.6」で絶対値の中がマイナスになるので、()の前に-をつけているのです。
だんだん絶対値がわかってきましたね。では問題をレベルアップしましょう!
『|x+4|=5x』
この問題が難しいのは、絶対値の中が+なのか-(マイナス)なのかわからないところです。
なので、このような絶対値の中にxなど文字がある問題は、絶対値の中が+の場合と-の場合に分ける必要があります。では問題の解説に入ります。
1、|x+4|が+または0である条件は、xが-4以上のときです。つまり、
x≧-4のとき、x+4=5x これを解くと x=1
このx=1は-4以上の条件を満たしています。
2、 |x+4|が -(マイナス)である条件は、xが-4よりも小さい数字であるときです。つまり、
x<-4のとき、-(x+4)=5x これを解くと x=-2/3
この x=-2/3 は-4よりも小さい条件を満たしていません。
よって、この問題の求める解は x=1 となります。
さぁ、皆さんどうでしょう?絶対値の問題が何となく理解できたでしょうか?
次の記事では絶対値の応用問題の解説をしていきますので、ぜひ次の記事と合わせて絶対値を攻略しましょう!


