こんにちは!塾長の坂根です。
今回は三角関数の最後の関門、『三角関数の合成』について解説します。『三角関数の合成』はどうやって求めるのかすぐに忘れてしまいますし、分かりづらい単元でもあります。しかし、三角関数の問題は合成がらみの問題がほとんどなので、ここで基礎をしっかり理解しましょう!
三角関数の合成の求め方
まずは三角関数の合成の求め方を見ていきましょう。
「asinθ+bcosθについて、半径をrとすると、
r=√aの2乗+√bの2乗
a= sinθ ,b= cosθ より、次のように式変形ができる。
asinθ+bcosθ =r( sinθ cosα+ cosθ sinα)=r sin(θ+α)」
はい!この時点でグロッキーぎみになるので、実際にグラフと問題を使って解説しますね。
「次の式を r sin(θ+α) の形に変形しなさい。ただし、r>0、-π<α<πとする。」
sinθ+√3cosθ
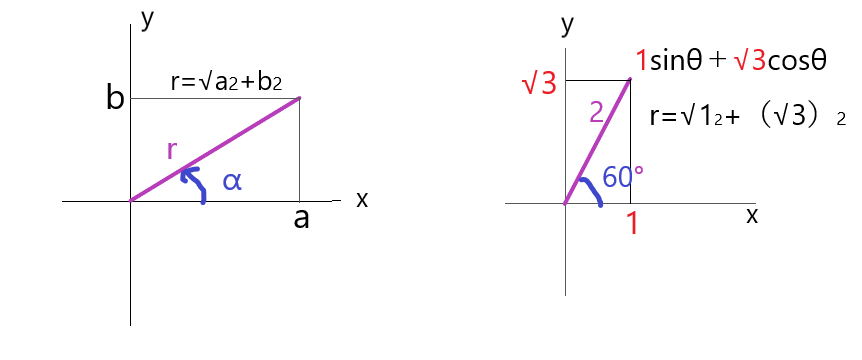
左のグラフが公式で、右のグラフが問題を公式にあてはめたものです。まず「r」の部分はsinθとcosθの係数を2乗して足します。
次にx座標は sinθ の係数、y座標は cosθ の係数になるように半径rの座標を書き、その半径とx座標がなす角が何度になるか考えます。この問題では、
r=√1の2乗+√3の2乗=√4=2
半径とx座標がなす角は60°になるためπ/3となります。よって変形した形は、
2sin(θ+ π/3 )
となります。
公式にあてはめるというより、グラフに書いた方がやりやすいと思います。
では次の問題に入ります。
「0≦θ<2πとするとき、方程式 sinθ+√3cosθ =1を満たすθの値を求めなさい。」
このような問題では三角関数の合成をしてから問題を解いていきます。先ほど変形したものを使って問題を解いていくと、
sinθ+√3cosθ =1 より、
2sin(θ+ π/3 ) =1 つまり、 sin(θ+ π/3 ) = 1/2
以前の記事で書いたように、三角関数はθの範囲を問題に合わせていくので、
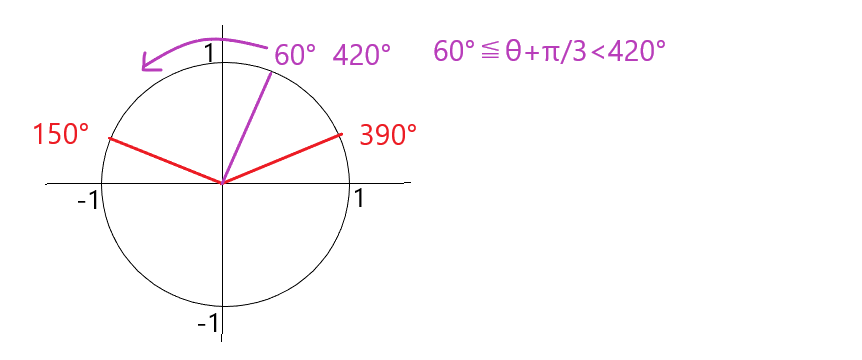
0≦θ<2π より、π/3≦ θ+ π/3 <7/3π(60°から420°の範囲)であるため、グラフより、
θ+ π/3=5π/6(150°)、13π/6(390°)
よってこれを解くと、θ=π/2、11π/6
となります。
上の問題のようにわかりやすい角度(30°60°45°など)は簡単ですが、そうでない角度がきたときの問題もやっておきましょう。
「次の式を r sin(θ+α) の形で表すときのrとsinα、cosαの値と求めなさい。ただし、r>0とする。」
4sinθ+3cosθ
この問題ではわかりやすい角度が出てきません。そのような場合でもグラフに書けば合成しやすくなります。
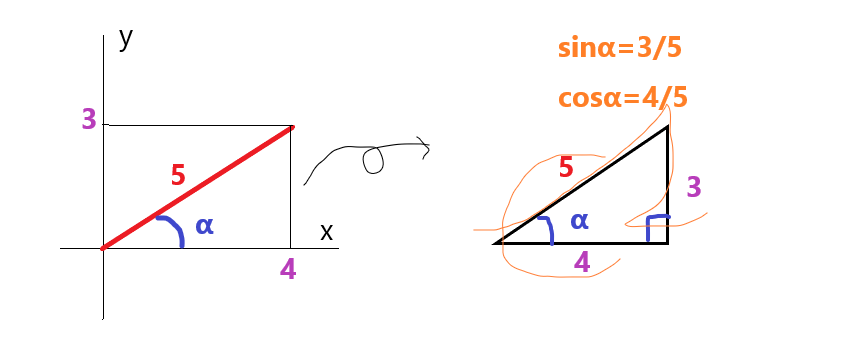
半径rは r=√4の2乗+√3の2乗=16+9=√25=5
またx座標は4,y座標は3をとるので、ここからは右の図のように三角比にあてはめるだけです。
ということで答えは、
sinα=3/5 cosα=4/5
となります。下手に公式にあてはめるよりも簡単にできましたね。
三角関数の合成を使った最大値・最小値
三角関数の合成でよく出る問題は最大値・最小値を求める問題です。2次関数を使った最大値・最小値を求める問題も出ますが、入試に出る頻度としては合成を使ったもののほうが多い傾向があります。では実際に問題を解いていきましょう。
「 0≦θ<πとするとき 、関数y=sinθ+cosθの最大値・最小値とそのときのθの値を求めなさい。」
まず、sinθとcosθは範囲が次のように決まっています。
- -1≦sinθ≦1
- -1≦cosθ≦1
グラフでもわかるようにy軸もx軸も1と-1の範囲におさまっていますね。ということは、yの最大値と最小値はこの「-1と1」の範囲を超えることは基本的にないということになります。このことを踏まえてグラフを見てみます。
まず合成して形を変形すると
y= sinθ+cosθ =√2sin(θ+π/4)
となります。
今回のθの範囲が 0≦θ<π と180°までということに注意してθの範囲を調整すると、
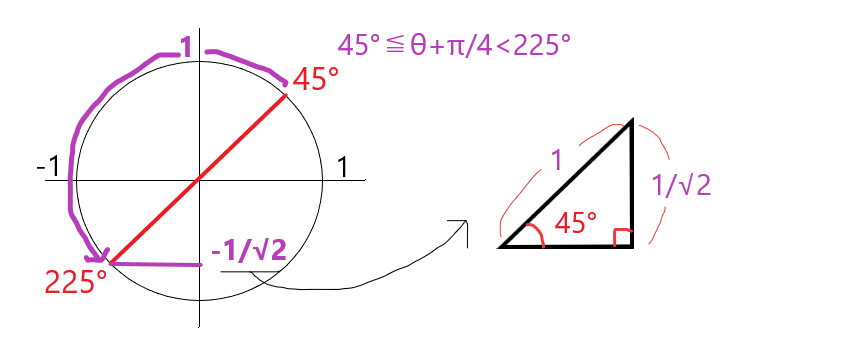
π/4≦ θ+π/4 ≦5π/4となります。グラフでいうと45°から225°の範囲です。
グラフのように、yの最大値は1ですが、最小値は225°までしか範囲がないため-1より手前になります。最小値yの求め方は右の図のように45°の三角比(三平方の定理)に入れると、
1:√2=y:1
つまりy=1/√2となります。よって、
sin(θ+π/4) =1より、 θ+π/4 =π/2のときyは最大
sin(θ+π/4) = -1/√2より、 θ+π/4 = 5π/4のときyは最小
最終的な最小値と最大値の求め方は、
-1/√2≦sinθ≦1より、左右にr=√2をかけて -1≦sinθ≦√2
したがって解答は、
θ=π/4のとき最大値√2、θ=πのとき最小値-1
三角関数まとめ
ここまで4回にわたって三角関数で皆さんがつまづきやすいところを解説してきましたが、三角関数の基礎が理解できたでしょうか?私の塾での高校生たちも三角関数が苦手な人が多いので、普段の授業のようにものすごく嚙み砕いて解説したつもりです。かみ砕き過ぎて数学の専門の人から見たら間違った解釈もあると思いますが、数学は答えが合っていればそれで良いと私は思っています(証明は除く)。
この記事ではド理系の学生さんでなく、文系で数学が苦手な学生さん向けに書いていますので、この記事で基本がわかってきたらテキストや過去問で応用問題にも挑戦してみましょう!



