こんにちは!塾長の坂根です。
今日は皆さん苦手な『三角関数』について解説していきます。
私も高校時代の数字で数列と同じぐらい苦手でした。しかし、三角関数の問題パターンは決まり切っているので、何点か重要なところを押さえていれば解ける問題が多いです。ここで三角関数を理解して、得点源にしましょう!
三角関数で皆さんが最初につまづく、というより公式を忘れる『三角関数の性質』について解説します。私の塾でも「公式ばっかりで覚えられない!」という声をよく聞きますが、あれは公式と言えるほどのものではなく、ごく当たり前のことを難しく書いてあるだけなのです。
では問題を例に考えてみましょう!「次の4つのとき、sinθ、cosθ、tanθの値を求めなさい」
①θ=7π/3
②θ=-π/4
③θ=7π/6
④θ=5π/8
まず三角関数で必ず押さえておかなければならないのは、 sinθ、cosθ、tanθ の符号です。これは座標の場所によってそれぞれの符号が決まっています。
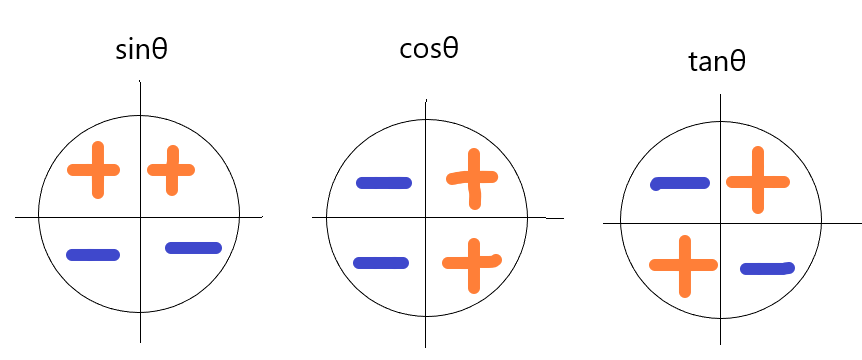
この符号の場所は皆さんよく知っていることだと思います。では、上の問題の解説に参ります。
一番わかりやすいのは①②の問題の場合です。グラフで表すとこんな感じです。
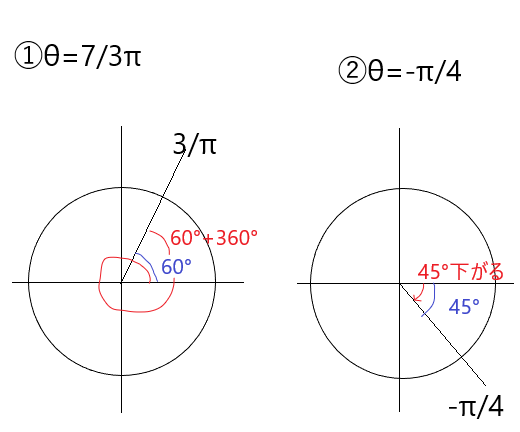
①のπの位置がおかしいですね(;^ω^)。正確には7π/3とπ/3です。すみません!
7π/3 は420°です。ということは、360°より大きいので2週目ということですね。三角関数は一周するとリセットされるので、60°の位置= π/3 で固定されます。これを式にすると、
sin(60°+360°)=sin60°=sin π/3 =√3/2
sin60°ということは、cosθ=1/2 tanθ=√3 になります。
これを公式っぽく書くとこうです。
sin(θ+2nπ)=sinθ
cos(θ+2nπ)=cosθ
tan(θ+2nπ)=tanθ
②はもっとわかりやすいですね。-があればその角度分下がればいいのです。
ただここから注意なのは、 sinθ、cosθ、tanθ の符号が変わっていくことです。角度がどの場所にあるのか確認していきます。
下がった場所はsinθとtanθが-(マイナス)でcosθは+です。なので式は、
sin(-45°)=–1/√2 cos (-45°) = 1/√2 tan (-45°) =–1
となります。
次は③④も問題です。とくに④が一番わかりづらいですよね(泣)。

③の場合は、7π/6=210°なので、180°を超えている位置にあります。そして、この場所は
sinθとcosθが-(マイナス)でtanθが+です。式にすると、
sin(30°+180°)=–sin30°=-1/2 –cos30°=–√3/2 tan30°=1/√3
になります。公式は下のようになります。
sin(θ+π)=-sinθ
cos(θ+π)=-cosθ
tan(θ+π)=tanθ
①と③からわかることは、「180°を超えているか360°を超えているか考えるだけ」です。
一番わかりづらい④の解説にいきましょう。ちなみに④の問題にはつぎの条件が入ります。
「0とπ/2の間の角の三角関数で表しなさい」
なぜこの条件が付くかというと、5π/8は30°や60°のような綺麗な値が出ないからです。そして、「0と90°の間」という言葉が入る場合、「+π/2(90°)して5π/8」になる数を考えます。その数はπ/8です。
そして一番面倒なのは、答えが単純に sinθ、cosθ、tanθ にならないことです。公式を見てください。
sin(θ+π/2)=cosθ
cos(θ+π/2)=-sinθ
tan(θ+π/2)=-1/tanθ
「なぜcosとかも変われば符号もバラバラなんだよ!」という憤りの声が聞こえてくるやつです。このときだけ大人しく公式を覚えるしかなさそうですが、一応解説しますね。
ここで鍵となるのは、 5π/8 ではなく 5π/8 のy軸と対象にある座標です。この座標を(x,y)とします。この座標が90°下がった位置の座標をみてください。座標がyとxの位置が入れ替わっています。
座標にすると(-y,x)となります。
さらに思い出してもらいたのが、 sinθ、cosθ、tanθ をx,y座標で表したものです。
sinθ=y/r(rは半径)、cosθ=x/r 、tanθ=y/x
+π/2の場合はそれぞれxとyが入れ替わることになるので、答えもそれに伴います。また、座標の位置は右下なので、これらを式にすると、
sin(π/8+π/2)=cosπ/8
cos (π/8+π/2)=‐ sinπ/8
tan (π/8+π/2)= -1/tanπ/8
最後の④だけまだよくわからないという方は、このときだけ公式を覚えるでもいいと思います。逆にいうと、残り3つは公式と言えるほどのものではないですからね。
今後の記事でも三角関数の解説記事を出していきますので、三角関数の苦手意識を克服しましょう!



