こんにちは!塾長の坂根です。
今日は三角関数第2弾!みんなが苦手な三角関数のグラフについて解説していきます。
三角関数のグラフは、今までのセンター試験のようなマーク式問題にはほとんど出てこなかったので、がっつり勉強している人はいなかったと思います。しかし、共通テストになってから数学ⅡBのマーク式問題では選択式の解答が多く、三角関数のグラフの問題の頻度が上がりました。なので、三角関数のグラフの応用問題ができないと点が取れません。
この記事では最後にグラフの応用問題の解説しますので、まずは三角関数のグラフの基本を押さえましょう。(この記事ではsinθとcosθのグラフを扱います)
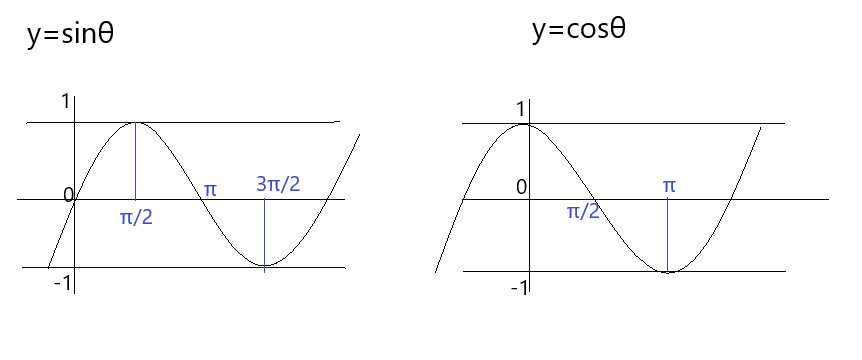
教科書に載っている基本のグラフですね。このグラフを変形させていきます。次のグラフを書いてみてください。
①y=2sinθ
②y=sinθ/2
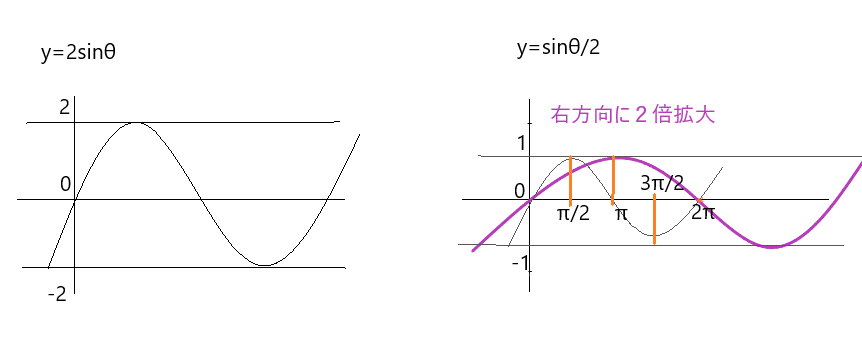
①のグラフのように、 y=asinθ はy軸方向(上下)にa倍になります。
②のグラフは、 y=sinkθはθ軸(右方向)に1/k倍拡大・縮小します。ここでは1/2θになっているので、θ軸方向に2倍拡大します。
なので、π/2の座標だった位置は「 π/2 ×2=π」のように、もとのグラフのθ座標×2をします。
さらに問題の難易度を上げます。次のグラフを書いてみてください。
y=2cos(θ/2-π/6)
みなさん「無理!」となるグラフですね。「何がどうなっているんだ」というグラフなので、一つ一つ手順を踏んでグラフを完成させます。
まずはこの式のままだとグラフが書けないので、上のグラフの形に近づけます。
y=2cos(θ/2-π/6) =2cos1/2(θ-π/3)
1/2を()の中からくくりだすことで、y=cosθ/2のグラフのようにします。
ここからは少しずつグラフを変形させていきます。
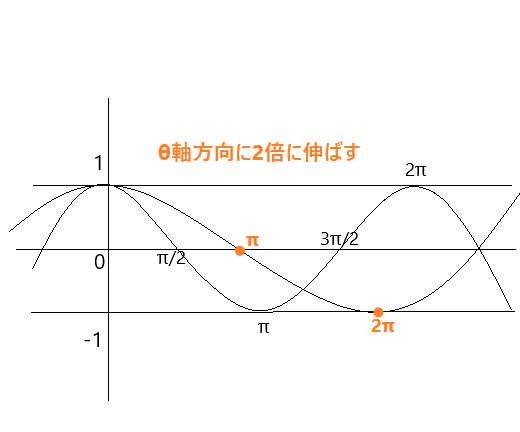
(グラフのπと2πの位置がずれていますが、本当は一致しています(;^ω^))。
最初に y=cosθ/2 のグラフを書くので、右方向にそれぞれのθ座標を2倍します。
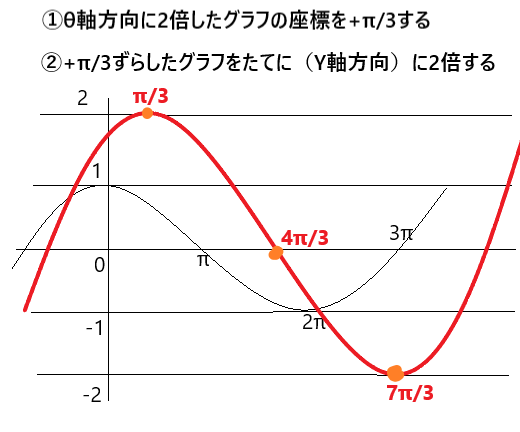
次に y=cosθ/2 のθ座標をπ/3足します。( θ-π/3 )から 「π/3 」が来ていますが、ここで注意なのは符号です。()の中の符号とは逆に移動させますので、もし ( θ+π/3 )なら-π/3します。
座標を式にすると、「π+ π/3 =4π/3」「2π+π/3=7π/3」
最後にy軸方向(上下)を2倍して完成です。
いかがでしょうか。一つ一つグラフを動かしていくとちゃんと答えのグラフになります。いきなりグラフを書こうとするのではなく、こういった地味な作業が正確な答えを導くのです。
これでもし記述やマーク模試で三角関数のグラフが問題になっても焦らず対応できると思います。
実際に教科書や問題集を使ってたくさんグラフを書いてみましょう!



