こんにちは!塾長の坂根です。
今回は「物理基礎」について解説していきます。私が一番苦手な科目、それが
「理科」
なのですが、そんな理科ポンコツの私でも実際に教えないといけないので、小学生の理科から勉強し直したところ、「物理」が一番わかりやすいなと思いました。物理が苦手な人が文系の人を中心に多いと思いますが、そんな人でもわかるように解説していこうと思います。ちなみに私の高校時代はまだ「基礎科目」がなく、物理は全く高校で習っていません。
物理を数学で解く方法① 運動
まず、なぜ物理分野が一番わかりやすいかというと、公式にあてはめれば解ける問題が多い点と、生物と化学は連動した問題が多い一方、物理は物理分野だけで問題パターンが決まっている点です。そして、物理分野は数学の知識で解ける問題も多く、数学は得意だけど理科は苦手という人は数学の知識で解いてみてください。例えば次の問題を解いてみましょう。
「はじめ止まっていた自転車が一定の加速度で加速したところ、3秒後に速さが6m/sになった。このときの、加速度の大きさと進んだ距離を求めよ。」
加速度の単元には次のような公式があります。
・v=v0+at
・s=v0t+1/2at2(2乗)
この公式をはじめ見たとき、「公式覚えてなかったらできなくね?」と思いました。しかし、グラフで表すとそんなに難しくないことがわかりました。この問題をグラフに表すとこのようになります。
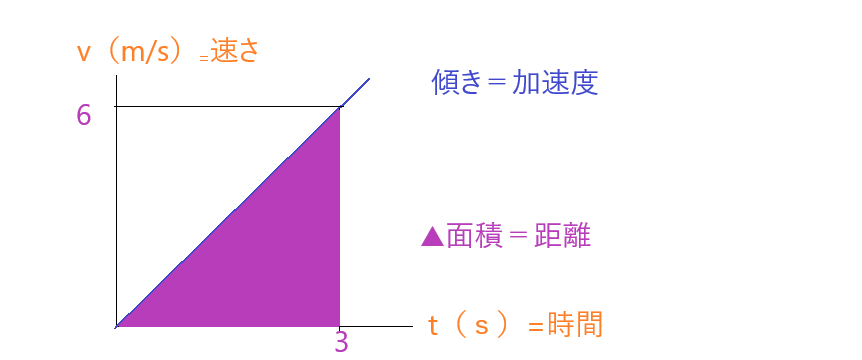
0秒から3秒後に速さが 6m/s になるため、グラフに表すと比例になります。加速度は比例の傾きとなるため、以前の「傾き」の記事でも書いたように「よこに3,たてに6」を読み取ると、
加速度=6/3=2m/s2(2乗)
となります。
距離は塗りつぶした面積になるため、
距離=3×6÷2=9m
となります。
これをさらに応用すると、次の問題も簡単に解けます。
「下の図のように直線上を運動する物体が、時刻t=0sからt=50sの間移動したときの距離と、平均の速度を求めよ。」

最初の問題のように、面積部分が距離になるため、
台形の面積は350m
となります。
平均の速度は「距離・時間・速さ」の公式にあてはめるだけなので、
速さ=350m(距離)÷50s(時間t)=7m/s
となります。
ちなみに、上の2つの問題は実際にセンター試験で出たものですが、複雑な計算は一切なかったですよね。
物理を数学で解く方法② 波の要素
次の単元は『波』です。「波」は中学校の理科では振動数や音の高低ぐらいしかなかったのですが、高校の物理基礎のレベルになると計算やグラフの読み取りが出てきます。もちろん中学校の波よりも難しくなるのですが、この「波」をグラフにすると「三角関数」のグラフと同じになるので、三角関数のグラフの問題を解くのに似ています。ただ厄介なのは、物理基礎は高校1年で履修する学校が多く、三角関数は物理基礎よりも後で習う単元なので、三角関数の知識で解くことができないのです。
波のグラフは以下のようになります。
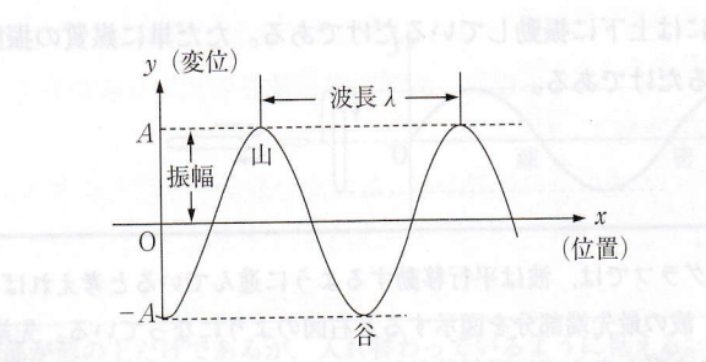
波長は三角関数でいうと「周期」と一致します。また、音の速さv[m/s]、周期T[s]、波長λ(読み方はラムダ)[m]、振動数f[Hz]は次の式が成り立ちます。
v=λ/T=f×λ
この公式は覚えやすいのでしっかり暗記しましょう。では実際に問題に入ります。
「下の図の波の速さは4㎝/sであった。この波の波長、振幅、振動数の値をそれぞれ求めよ。」
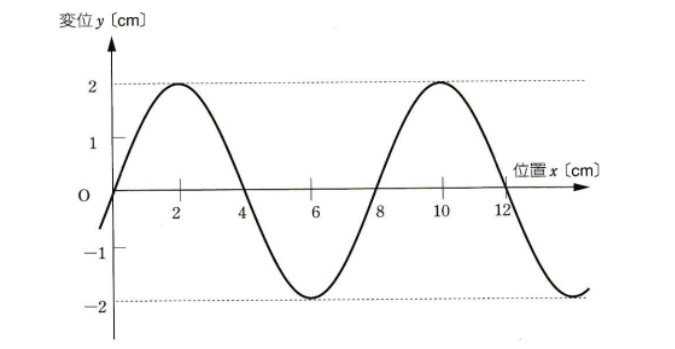
波長と振幅はそのまま読み取ればいいですよね。波長は周期と同じなので、
波長=8
振幅=2
となります。
振動数は公式にあてはめると
v=f×λより、f=v÷λ=4cm/s÷8(波長)=0.5(Hz)
となります。
まとめ
物理がすべて数学の知識で解けるわけではありません。しかし、実際に私が高校生に物理基礎を教えるときはほぼ数学の問題と同じように解いています。それは私自身が高校物理を習っていないことが一番大きいと思います。物理として習っていない以上、数学の問題として捉えるしかなく、逆に生徒にとっては数学の問題と同じなんだと理解しやすくなっています。
ただ、物理基礎の難しい点は先ほど書いたように、数学ⅡBの知識があれば簡単に解けるのに、数学よりも物理基礎の方が先に授業が始まってしまう点です。この点に関しては実際に高校で物理を教えている先生方も同じように思われているようです。こればかりは学習指導要領の問題なのでどうしようもないですね。しかし、数学をしっかり理解した後に物理の問題を見ると、かなり物理の問題が解きやすくなると思うので、私が以前の記事で書いた「三角関数」などを読み直して、物理の問題に挑戦してみてください。今後は他の物理の単元の解説も行っていきます。



