こんにちは!塾長の坂根です。
今日は前回の記事でも書いた『2次関数の最小値・最大値の場合分け』の仕方第2弾です。
今回は定義域が文字になっていて、定義域が動いていくパターンを解説していきます。
まずは次の問題を解いてみてください。
「aは正の定数とする。定義域が0≦x≦aである関数y=x2(xの2乗)-4x+1の最大値および最小値を求めよ。」
この関数の頂点は(2,-3)、軸はx=2です。そして、切片の記事で書いたように必ずy軸は「1」を通る関数です。
前回の記事でも触れましたが、2次関数の最小値・最大値の場合分けの攻略の仕方は、「定義域の真ん中と軸の位置関係」です。
では実際にグラフにして場合分けしましょう。
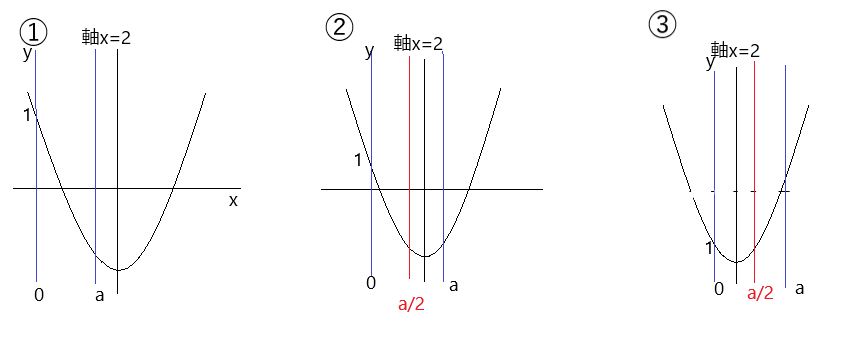
今回の問題は軸がx=2で固定され、定義域の小さい方(左側)は「0」なのでy軸と定義域の左は一致します。
①は最大値が0のとき、最小値はaのときです。このときのaの条件は「軸よりaが小さい、そしてaは0より小さくはならない」です。
つまり、0<a<2のとき、x=0で最大値1 x=aで最小値a2-4a+1
②は 最大値が0のとき 、最小値は頂点のときです。このときのaの条件は「定義域の真ん中a/2(0とaの半分はa/2)とaの間に軸(x=2)があるとき」です。
つまり、a/2<2→a<4かつ2≦aなので、 2≦a<4 のとき x=0で最大値1 x=2で最小値-3
③は最大値がaのとき、最小値は頂点です。このときの aの条件は 「定義域の真ん中a/2より軸が小さい(左側)のとき」です。
つまり、2<a/2なので、4<aのとき x=aで最大値a2-4a+1 x=2で最小値-3
④最後は軸と定義域の真ん中が一致するときなので下のようなグラフです。

最大値は0と4(軸が2なので、軸と左右対称のx座標は0と4)のとき、最小値は頂点のときです。このときのaの条件は「軸x=2とa/2が一致するとき」です。
つまり、a=4のときx=0,4で最大値1 x=2で最小値-3
模試や大学受験では定義域の方または関数のどちらかがわかっていない場合がほとんどで、自分で場合分けする必要があります。とくに定義域がわかっていない(文字がある)ときは、上の図のように
定義域の両サイドを足して2で割ったもの〈例〉(a+a+2)÷2 が真ん中なので、
「その値より軸が小さい(左)か大きい(右)」がポイントになります。
今までの書いた「2次関数の最小値・最大値の場合分け」と「切片」の記事を合わせて読んでもらえると、より正確なグラフが書けて問題が解けやすくなります。
2次関数の問題は必答問題かつ他の単元と合わせて出される重要な単元なので、今後の記事でも解説していきます!


