こんにちは!塾長の坂根です。
今日は、高校数学でみんなが最初にぶち当たる壁『2次関数の最小・最大値の場合分け』について解説していきます。
模試や共通テスト(センター試験)にも必ずと言ってもいいぐらい出てくる2次関数ですが、関数や定義域に「a」などの文字が入ってきた瞬間、「あぁ、あのよくわからないやつきた…」となる人が多いですよね。
皆さんが2次関数で苦手意識を持っているのは、大体「定義域があって、aなどの文字を含む関数の場合分け」だと思います。そして、前回の『絶対値』でも出た「場合分け」の仕方がわからない人が一番多いと思うので、その「場合分け」の仕方を中心に解説していきます。
まず2次関数の場合分けのポイントは、5つの定義域パターンを押さえていることと、そのパターンは軸(x=頂点)が基準になっていることです。5つの定義域パターンは下の通りです。
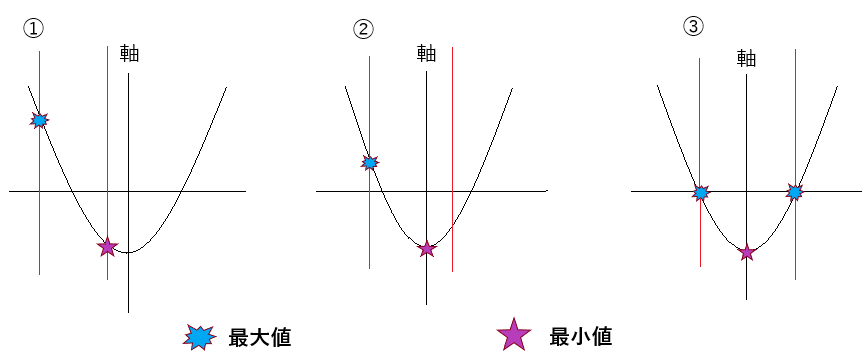
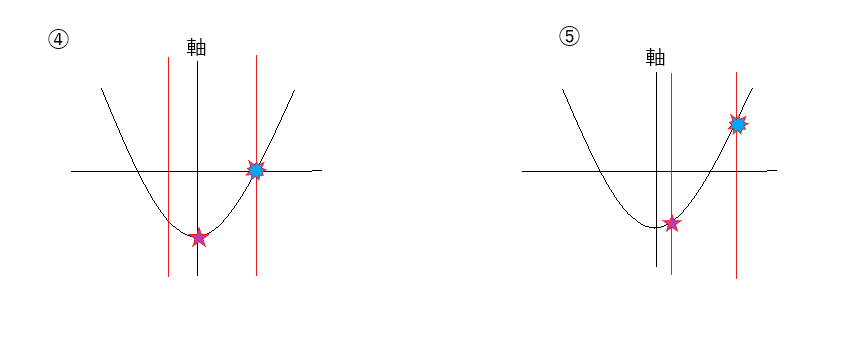
上のグラフのように、定義域がだんだん右にずれていくのがわかりますね。さらに、そのずれ方は大きく3つに分けて、「軸より完全に左側(軸より小さい)」・「定義域の中に軸がある」・「軸より完全に右側(軸より大きい)」に分かれます。
2次関数のグラフを定義域別に書いて最小・最大値を求めるときに、一番わかりやすいのが「定義域が軸よりも完全に右か左にいるとき」です。上のグラフで言うと、①と⑤ですね。
なぜかというと、最大値もしくは最小値は定義域の右か左側(0≦x≦2なら0か2のとき)最小値・最大値)になるからです。
一方わかりにくいのが「定義域の中に軸が入ってきた」とき(上のグラフで言うと②③④)です。しかし、この場合は最小値(a>0で下に凸のとき)・最大値(a<0で上に凸のとき)は常に頂点になります。そして、もう一方の最小値・最大値は定義域が軸の右か左のどっちかに寄っていて、軸から離れている方になります。③のグラフは定義域が左右対称の位置になるのでどちらも最大値です。
最小値・最大値はグラフを書くとわかりやすいですね。では続いて、皆さんが一番苦手な「a≦〇のとき~」の仕方を、実際の問題を解きながら理解していきましょう。
「aは定数とする。0≦x≦4における関数f(x)=X2(xの2乗)-2ax+3aについて、最小値・最大値を求めよ」
関数の式を平方完成すると、頂点(a,-a2+3a) 軸x=a
aの範囲の場合分けのポイントは、「定義域の真ん中を基準にして軸がどこにあるか」です。
まず、上のグラフでいう①⑤の場合は最小値・最大値はわかりやすいですね。最小値は
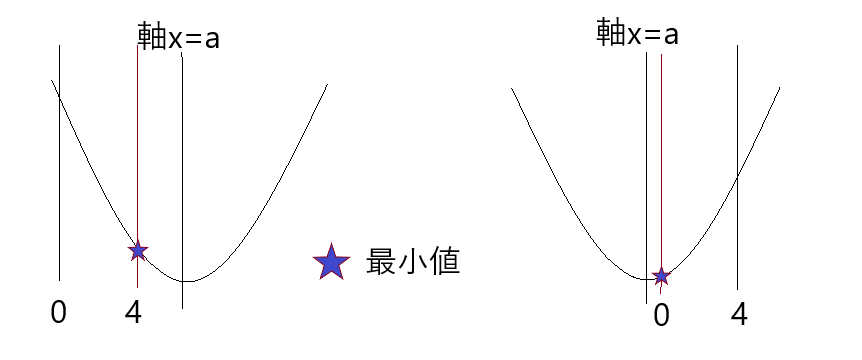
左のグラフはx=4のとき最小値で、そのときの条件は「4よりも軸が右にある」
つまり、a>4のとき x=4 で最小値
右のグラフはx=0のとき最小値で、そのときの条件は「0よりも軸が左にある」
つまり、a<0のとき x=0で最小値
つぎに、定義域に軸が入ってきたときのグラフは下の通りです。
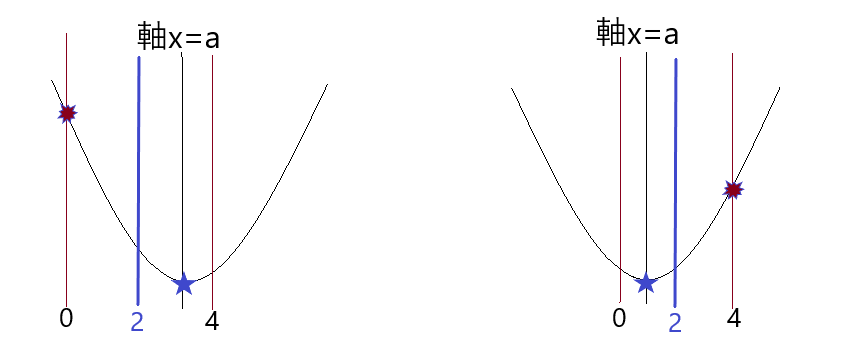
定義域内に軸がある限り、最小値は頂点になります。
つまり、0≦a≦4のとき x=aで最小値
最大値のポイントは先ほど言った通り、「定義域の真ん中」です。今回の問題の定義域の真ん中は2です。左のグラフと先ほどの左側グラフのように、「軸が2と4の間にあるとき、軸が4より左にあるとき最大値は0の場所」
つまり、a>2のとき(aが2より左にあるとき) x=0で最大値
また、上2つの右側のグラフのように、「軸が0と2の間、軸が0より右にあるとき最大値は4の場所」
つまり、a<2(aが2より右にあるとき) x=4で最大値
最後のグラフは、定義域のど真ん中に軸があるグラフです。
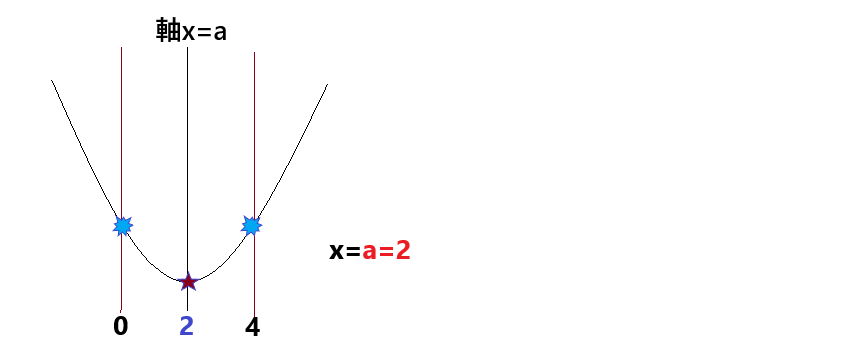
最大値は0と4が同じ位置にあるときなので、「軸と定義域の真ん中が一致するとき最大値は0と4の場所」
つまり、a=2のとき x=0,4で最大値
以上をまとめると、
「最大値は2(定義域の真ん中)を基準にして考える」
「最小値は定義域の小さい方(0)か大きい方(4)を基準にして考える」
ということになります。
このようにして2次関数の場合分けをしていきます。ちなみに今回は省きましたが、最小値・最大値の値はyの値なので、xの値を関数の式に代入したものになります。
今回は下に凸バージョンでしたが、上に凸の場合が最小値・最大値の考え方が逆になります。
とにかく大事なのは、2次関数の問題は必ずグラフを書くことです。書けばわかりやすくなるので、この記事や教科書にあるグラフをもとに自分で実際に書いて練習しましょう!


