こんにちは!塾長の坂根です。
今日は一次関数のグラフの『傾き』の解説と応用方法をお伝えします。
まず実際のグラフを見て傾きの確認をしましょう。
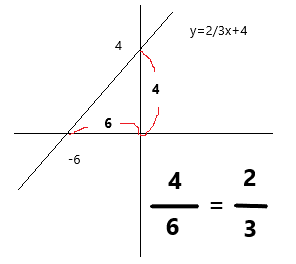
傾きは上のグラフのようにxの前にある2/3で、直線がどれだけ斜めっているかを数字化したものです。
傾きは数学の世界では『変化の割合』とも言いますね。中学数学では『変化の割合』はこのように公式になっています。
『変化の割合= yの増加量/xの増加量 』
『yの増加量/xの増加量』と言われてもピンとこない方は、下のように覚えてみてください。
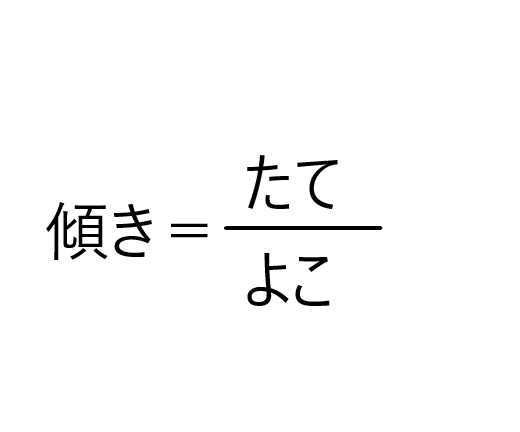
読み方は『よこ分のたて』です。上のグラフで説明すると、
『よこに6進んで、たてに4上がる』
ということです。約分すると傾きは2/3になります。グラフの傾きを書くのが微妙な方はこれでばっちりグラフが書けますね!
この『よこ分のたて』の知識さえあれば、どんな一次関数のグラフでも簡単に読み取ることができます。
実際に問題を見てみましょう。

(2)のバスの時速を求める問題が傾きを読みとって解くものです。横に10進んでたてに5上がっていますね。単純に『たて/よこ』に当てはめると1/2になってしまいますが、この問題は時間(x)が「分」になっているので「時間」にそろえましょう。
「分」から「時間」にする方法は『〇分/60分』の〇部分に10をあてはめます。すると「10/60=1/6」になります。
ここから 『たて/よこ』 にあてはめると、『5/ 1/6』になり、『5÷1/6=5×6=30』で答えは
『時速30㎞』になります。
この問題は中学数学ですが、高校の公式にも 『たて/よこ』 が出てきます。
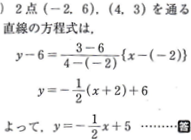
上の問題は2点を通る直線の方程式を求めるものです。
高校の傾きの公式では『傾きm=y2-y1/x2-x1』と一気にめんどくさい感じに公式化されてますが、
要は『よこ(x)に6進んで、たて(y)に3下がっている』と言っているだだけです。
この『傾き』のテクニックを知っているだけで解ける問題のバリエーションが増えます。色々な問題を解いているうちに、「傾きってそういうことを表しているのか」と自分で理解できてきますので、ぜひこのやり方を使ってみてくださいね。



