こんにちは!塾長の坂根です。
今回は三角関数第三弾!『三角関数を含む方程式・不等式』編です。この単元は何となくできるけどちゃんと理解していない人が多いですし、理解しないと今後の三角関数の応用ができなくなります。ここでしっかり基本を押さえておきましょう!
今回は手書きの図なので見づらいかもしれませんが、ご了承ください。
三角関数の方程式
まずは基本の方程式問題から解説します。(ここから出す図は『π』より『○○°』の方がわかりやすいので、『○○°』で表記しています)
では早速次の問題を解いてみてください。
「0≦θ<2πのとき、次の方程式を満たすθの値を求めよ。」
「(1)sinθ=-1/2 (2)cosθ=√3/2」
sinθ・cosθ・tanθの+と-の位置は前回の三角関数の記事で確認してください。そして、三角関数の問題で大切なのは「θの範囲」です。「0≦θ<2π」ということは「0°~360°未満がθの範囲」ということになります。では実際のグラフを見てください。
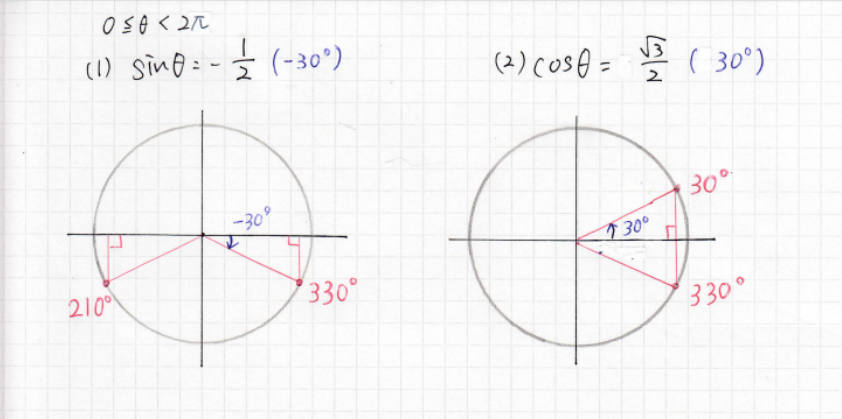
(1)の問題はsinθが-なので下半分の位置に座標があり、30°分下がった位置は330°なので11π/6、もう一方は210°の位置なので7π/6が座標にあたります。したがって答えは
θ=7π/6、11π/6
となります。
(2)の問題はcosθが+なので右半分の位置に座標があり、30°と330°の位置、つまりπ/6と11π/6の位置に座標があります。したがって答えは
θ=π/6、11π/6
となります。
少し問題を難しくします。
「0≦θ<2πのとき、次の方程式を満たすθの値を求めよ。」
「(3) sin2θ=1/2 (4)cos(θ-π/3)=-√3/2 」
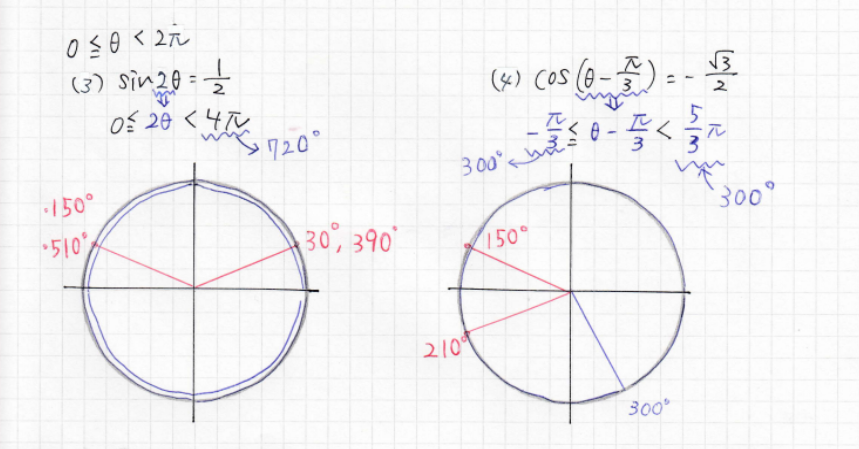
sinやcosの後ろがθでない場合は、「0≦θ<2π」のθを問題に合わせます。図でもあるように、真ん中のθを(3)なら2θにして両サイドも2倍に、(4)なら-π/3して両サイドも-π/3します (右は2π-π/3=5π/3)。
となると、θの範囲は「0°~360°未満」から図のような範囲にそれぞれなります。(3)の問題は2週目も範囲に入るため、座標は30°150°390°510°にあたります。したがって答えは
2θ=π/6、5π/6、13π/6、17π/6(2θにすることに注意)
θ=π/12、π/12、13π/12、17π/12
となります。
(4)は150°210°の位置に座標があるため、
θ-π/3=5π/6、7π/6(θ-π/3にすることに注意)
θ=7π/6、3π/2
となります。
三角関数の不等式
次は不等式の問題に入ります。次の問題を解いてみてください。
「0≦θ<2πのとき、(1)不等式sinθ>-1/2 (2)tanθ>1を満たすθの値の範囲を求めよ。」
三角関数の不等式の場合は、不等号が「>」のとき角度からsinθは上、cosθは右、tanθはy軸に向かってのエリアが範囲となります。「<」のときは逆ということです。では実際の図で説明します。
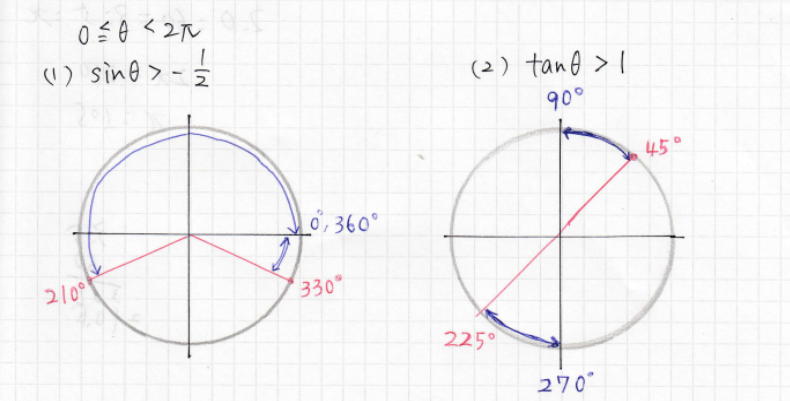
(1)(2)それぞれ青いエリアが範囲ということになります。ここで注意なのは、不等式の範囲を求めるとき、角度が0°以下(右下エリア)から始まるときは必ず「0≦θ」から範囲を求めます。(1)のように330°から上に向かって全範囲を求めたくなりますが、330°からの範囲は360°までになります。
したがって(1)の求め方は
0≦θ <7π/6、11π/6<θ<2π
となります。
(2)のtanθの場合は、+のエリアが右上と左下になるので、90°までと270°までの範囲となります。
したがって(2)の求め方は、
π/4<θ<π/2、5π/4 <θ< 3π/2
となります。
まとめ
今回は基本的な三角関数の方程式と不等式の解説をしました。今後はさらに他の三角関数でよくつまづくポイントを解説した後に受験問題レベルの問題の解説をしようと思います。大学受験レベルの問題はどんなに嚙み砕いても基本がわかっていないとチンプンカンプンなので、以前書いた三角関数の解説も読んで三角関数の基本をしっかり理解しましょう!



